画像 alternate interior corresponding angles theorem 194169-Alternate interior corresponding angles theorem

Answer choices r is parallel to s by converse of Alternate Interior Angles Thm u is parallel to v by Converse of Corresponding Angles Thm s is ⊥ u by Converse of Alternate Interior Angles Thm v ⊥ r by Converse of Alternate Exterior Angles Thm <p>r is parallel to s by converse of Alternate Interior Angles Thm</p>= 3 x 35 16Using corresponding angles theorem, ∠x has same measure with angles in the opposite, so it is x (vertical angles) ∠x (based on the previously reason) and ∠ (x40)°

Alternate Interior Angles Definition Theorem Examples Video

Alternate interior corresponding angles theorem

Alternate interior corresponding angles theorem-Because these lines are parallel, the theorem tells us that the alternate interior angles are congruent So, that means that angles 1 and 8 are congruent, or the same, and angles 2 and 7 areSide AB is parallel to side DC so the alternate interior angles, angle ABD and angle CDB, are congruent Side AB is equal to side DC and DB

Given The Information In The Diagram Which Theorem Best Justifies Why Lines J And K Must Be Brainly Com

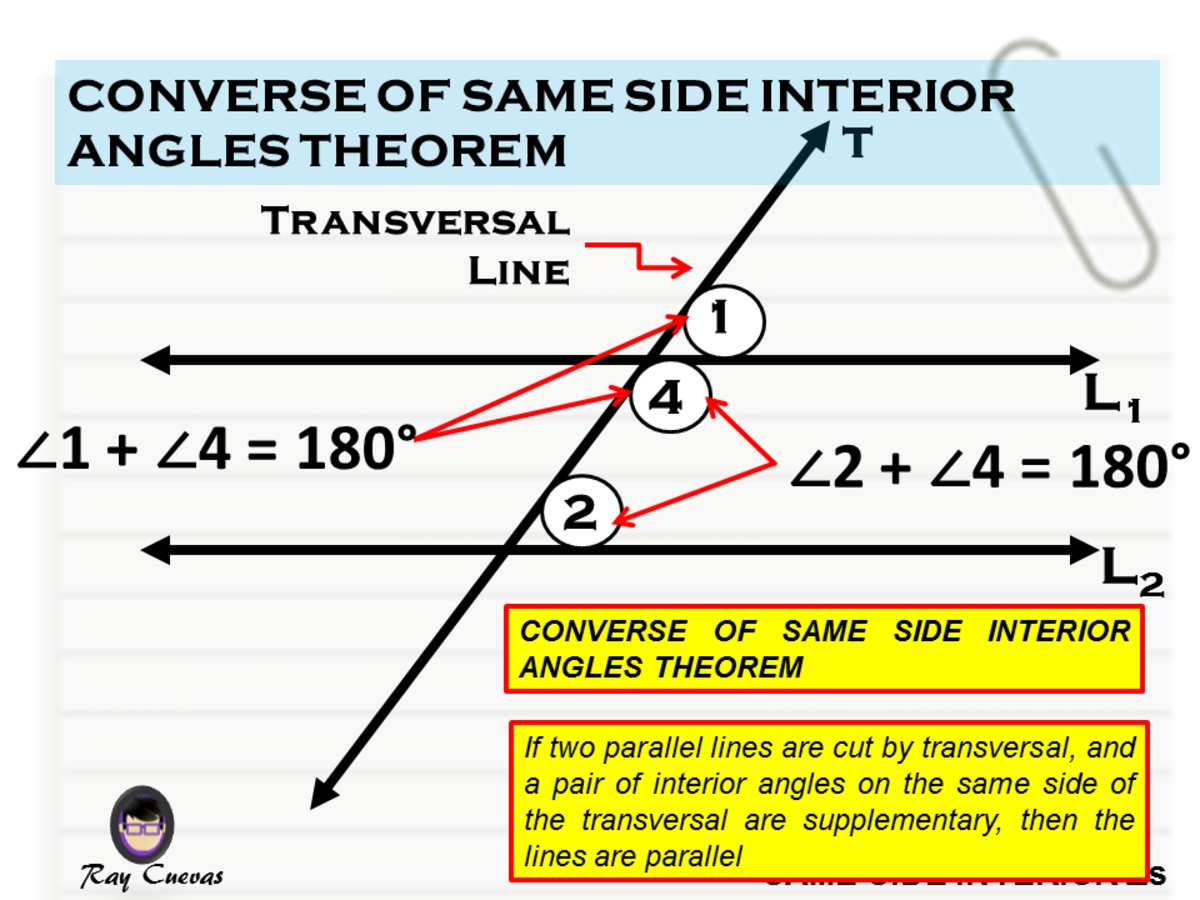
Converse of the Alternate Interior Angles Theorem If two coplanar lines are cut by a transversal so that a pair of alternate interior angles areConverse of the Alternate Interior Angles Theorem If two lines and a transversal form alternate interior angles that are congruent, then the two lines are parallel Converse to the Alternate Exterior Angles Theorem If two lines and a transversal form alternate exterior angles that are congruent, then the two lines are parallel Converse toWhat is the difference between properties of parallel Cheggcom Math Geometry Geometry questions and answers What is the difference between properties of parallel lines (ex corresponding angles theorem, alternate interior angle theorem, etc) versus their respective converse theorems (ex corresponding angles converse, alternattive angle

= (3x 16)°One way to find the alternate interior angles is toAlternate interior angles are formed when a transversal passes through two lines The angles that are formed on opposite sides of the transversal and inside the two lines are alternate interior angles The theorem says that when the lines are parallel, that the alternate interior angles are equal

Note that β and γ are also supplementary, since they form interior angles of parallel lines on the same side of the transversal T (from Same Side Interior Angles Theorem) Therefore, since γ = 180 α = 180 β, we know that α = β This can be proven for every pair of corresponding angles in the same way as outlined aboveThe sameside interior angles is a theorem which states that the sum of sameside interior angles is 180 degree When two parallel lines are intersected by a transversal line they formed 4 interior angles The 2 interior angles that are not adjacent and are on the same side of the transversal are supplementaryProperty CorrespondingAngles and the Parallel Lines AlternateInteriorAngles When two parallel lines are intersected by a transversal, angles that are formed in between (interior) the lines and on opposite sides of the transversal (alternate) form two pairs of alternateinteriorangles

How To Prove Corresponding Angles Are Congruent

Ppt Corresponding Angles Postulate Powerpoint Presentation Free Download Id

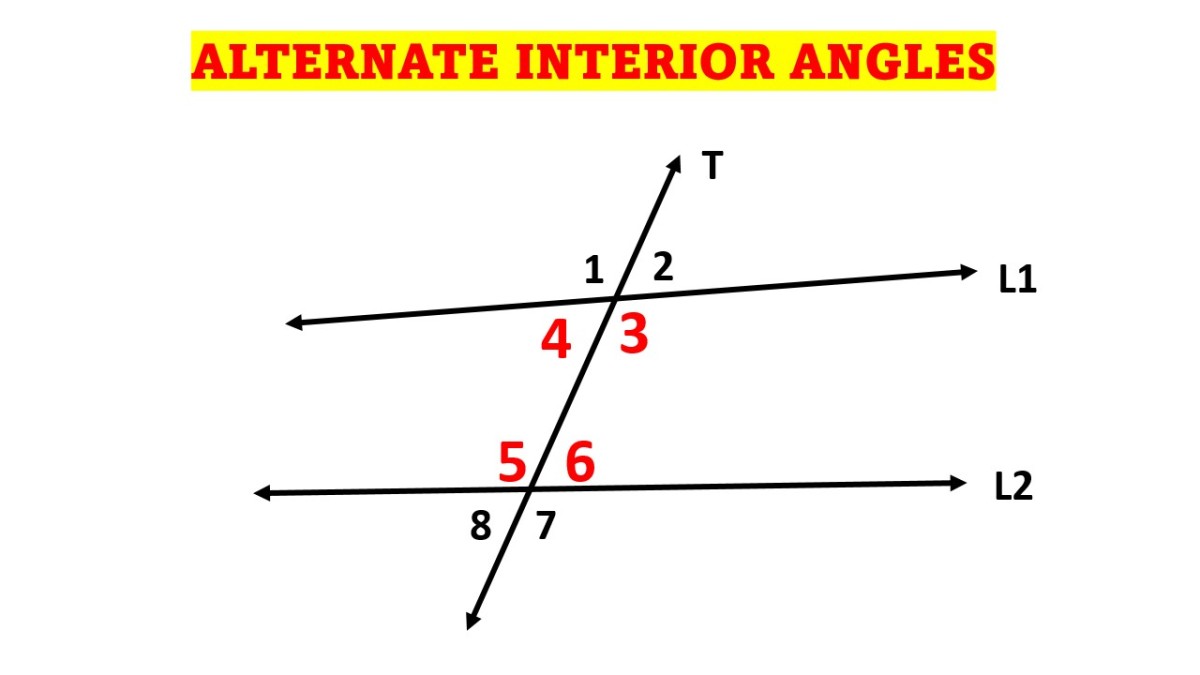
Alternate angles are shaped by the two parallel lines crossed by a transversal Consider the given figure, EF and GH are the two parallel lines RS is the transversal line that cuts EF at L and GH at M If two parallel lines are cut by a transversal, then the alternate angles are equal Therefore, ∠3 = ∠ 5 and ∠4 = ∠6Angle addition postulate If P is in the interior of <RST, then m<RSP m<PST = m<RST alternate interior angles angles between 2 lines and on opposite sides of a transversal consecutive interior angles two angles that lie between the two lines and onAlternate Interior Angles Theorem/Proof The theorem states that if a transversal crosses the set of parallel lines, the alternate interior angles are congruent

Square Barc For Parallel Descubre Como Resolverlo En Qanda

Geometry Angle Theorems Flashcards Quizlet

Exterior angles are a bit more tricky But basically, you can find an exterior angle by taking one of the lines on the polygon and extending it out further, beyond one of the other lines it intersects The new angle you get is called an exterior angle, because it is on the outside of the polygonAs a consequence of Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equalAlternate Exterior Angle Theorem;

Are Alternate Exterior Angles The Same

Same Side Interior Angles Definition Theorem Video Lesson Transcript Study Com

Solution 2 By corresponding angles theorem, angles on the transversal line are corresponding angles which are equal Thus exterior ∠ 110 degrees is equal to alternate exterior ie 110 degrees X is adjacent Making a semicircle, the total area of angle measures 180 degrees Thus 110 x = 180 X = 180 – 110 X= 70 degreesThe Alternate Interior Angles theorem states, if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent A theorem is a proven statement or anStatement for Alternate Interior Angles The Alternate interior angle theorem states that " if a transversal crosses the set of parallel lines, then the alternate interior angles are congruent" Given Line a is parallel to line b To prove We need to prove that angle 4 = angle 5 and angle 3 = angle 6

Properties Of Parallel Lines Postulate 15 Corresponding Angles

Alternate Interior Angles Definition The Education

Alternate Interior Angles Theorem Example 3 Find Solution because they are corresponding angles and the lines are parallel and are vertical angles, so also and the angle are alternate interior angles Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then the alternate interior angles are congruentAlternate exterior angles are created when three lines intersect A line that crosses two or more other lines is called a transversal Often, two of the lines will be parallel, setting up some interesting angles with the transversal When a transversal crosses two other lines, it creates an exterior and interior for the parallel linesAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &

Alternate Interior Angles Theorem Mathematical Objects Elementary Geometry

Alternate Exterior Angles Definition Theorem Examples Video

Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal In this example, these are two pairs of Alternate Interior AnglesThis relation is determined by the Alternate Interior Angle Theorem When a transversal intersects two parallel lines, each pair ofAlternate Interior Angle Theorem Suppose two parallel lines are intersected by a transversal, as shown below What is the relation between any pair of alternate interior angles?

Same Side Interior Angles Theorem Proof And Examples Owlcation

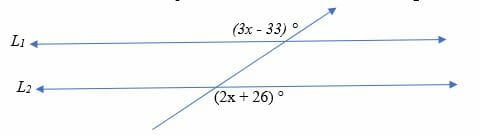
Alternate Exterior Angles Explanation Examples

A Use the Consecutive Interior Angles Converse Theorem B Use the Alternate Exterior Angles Converse Theorem C Use the Alternate Interior Angles Converse Theorem D Use the Corresponding Angles Converse Postulate 12 Use the diagram below in the following exercise How would you show that the lines a and b are parallel?(1 point) a) Alternate Interior Angles Theorem b) Corresponding Angles Postulate c) SameSide Interior Angles TheoremWhen the two lines intersected by the transversal are parallel, corresponding angles are congruent, alternate interior angles are congruent, alternate exterior angles are

Same Side Interior Angles Wild Country Fine Arts

Alternate Interior Angles Definition Theorem Examples Video

Safety How works Test new features Press Copyright Contact us Creators4 Theorem 34 If corresponding angles are congruent then the lines are parallel Proof of Theorem 34 Given Prove l//m 15 l m 5 1 4 Statements Reasons 1 Given 4 / /lm 2 m 1 4 180 m 0 2 Angles 1 and 4 form a linear pair 3 Substitution 1 1 5 4 Theorem 36 If sameside interior angles are supplementary then theDiscussion Section 1 3 Corresponding Angles Converse Alternate Interior Angles Definition Theorem Examples 1 Write A Proof Of The Alternate Exterior Angles Theorem Ppt 3 3 Proving Lines Parallel Powerpoint Presentation What Is The Converse Of The Alternate Interior Angles

Please Help A Proof Of The Alternate Interior Angles Theorem Using Parallel Lines A And B With Brainly Com

Answered Use The Folowing Diagram For The Bartleby

The alternate interior angles theorem states that "if a transversal crosses the set of parallel lines, the alternate interior angles are congruent" In the figure given below, a set of parallel lines \( m\) and \( n\) are intersected by the transversal and the following pairs of alternate interior anglesSo let's do exactly what we did when we proved the Alternate Interior Angles Theorem, but in reverse going from congruent alternate angels to showing congruent corresponding angles Proof Here's how you prove the converse of the Alternate Interior Angles Theorem (1) m∠5 = m∠3 //given (2) m∠1 = m∠3 //vertical, or opposite anglesTheorem – Converse If Exterior angles on the same side of the transversal sum to 180, then lines are parallel m<1m<8=180 Alternate Interior Angles Theorem – Converse If Alternate Interior angles have equal measure, then lines are parallel Angle 3 and Angle 5, Angle 4 and Angle 6 Angle 12 and Angle14

Alternate Exterior Angles Theorem Geogebra

Proof Consecutive Interior Angles Converse Youtube

Corresponding Angles Postulate, or CA Postulate If two parallel lines are cut by a transversal, then corresponding angles are congruent (Lesson 26) Alternate Interior Angles Theorem, or AIA Theorem If two parallel lines are cut by a transversal, then alternate interior angles are congruent (Lesson 26) Alternate Exterior Angles Theorem, orThe Alternate Interior Angles Theorem states that When two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent How to identify Alternate Interior Angles?Converse of the Alternate Interior Angles Theorem (333) If two coplanar lines are cut by a transversal so that a pair of alternate interior angles are congruent, then the two lines are parallel

Converse Of Same Side Consecutive Interior Angles Theorem Geogebra

Alternate Interior Angles Theorem And Examples Owlcation

Triangle Sum Theorem 3 Corresponding angle are congruent Triangle ABC is a right triangle Point D is the midpoint of side AB and point E is the midpoint of side AC The measure of angle ADE is 47°Alternate interior angles theorem If two parallel lines are cut by a transversal, then the alternate interior angles are congruent Corresponding angles theorem If two lines are cut by a transversal so the corresponding angles are congruent, then the lines are parallel Alternate exterior angles theoremThe Corresponding Angles Theorem says that If a transversal cuts two parallel lines, their corresponding angles are congruent The Corresponding Angles Postulate is simple, but it packs a punch because, with it, you can establish relationships for all eight angles of the figure

Corresponding Angles Defintion Theorem Examples Video

Mrwadeturner Consecutive And Alternate Exterior Angles

Alternate Interior Angles Theorem The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then alternate interior angles are congruent Alternate Interior Angles Theorem Proof Let L1 and L2 be parallel lines cut by a transversal T such that ∠1 and ∠3 are alternate interior anglesGiven the following information, state the postulate or theorem that justifies a b 5 371 4 5 44 and 6 are supplementary Solution Converse of the Corresponding Angles Postulate Converse of the Alternate interior Angles Theorem Converse of the Alternate Exterior Angles Theorem Converse ofSolution According to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines Thus, (4x – 19)°

Proof Consecutive Interior Angles Are Supplementary Youtube

Parallel Lines Theorems Notes Euclidean Plane Geometry Geometry

X 40 o x = 180 oThe Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent Converse of Alternate Interior Angles Theorem The converse of the theorem is also trueAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &

Can Someone Explain This I Just Need 3 6 Geometry

1

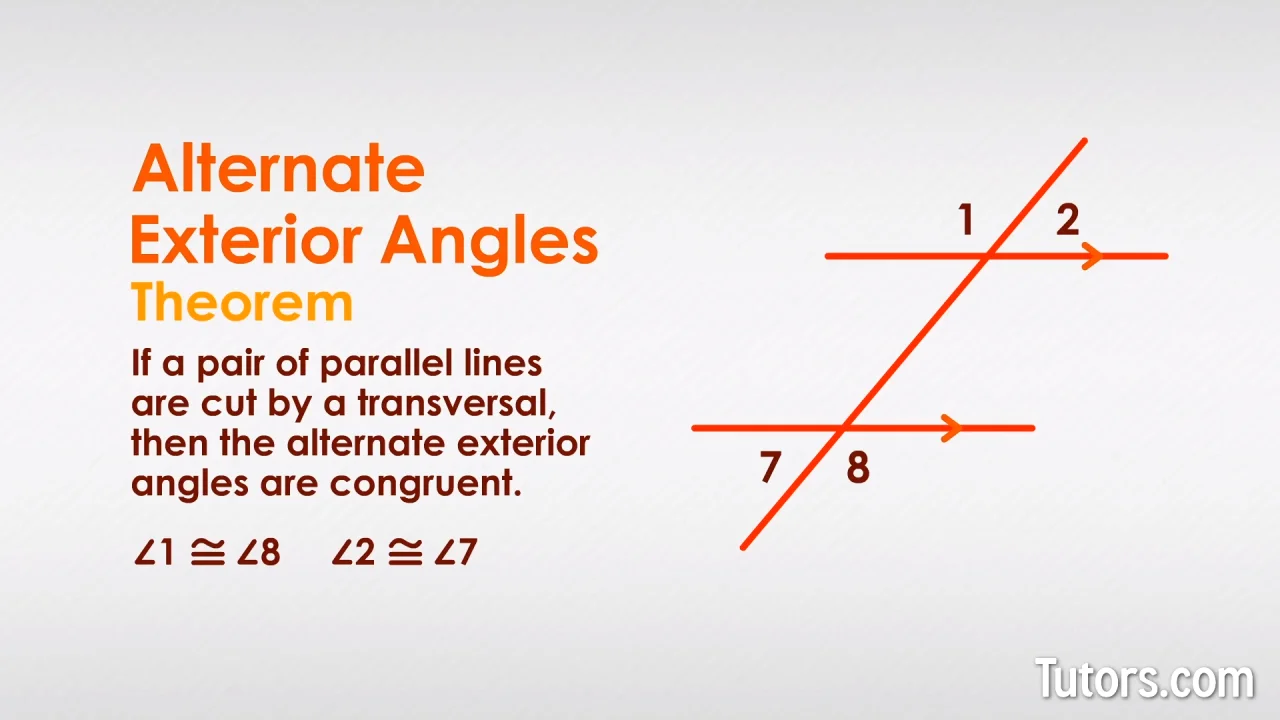
According to the converse of the alternate interior angles theorem, if a transversal intersects two lines such that the alternate interior angles are equal, then the two lines are said to be parallelThe Alternate Exterior Angles Theorem states that, when two parallel lines are cut by a transversal , the resulting alternate exterior angles are congruent So, in the figure below, if k ∥ l , then ∠ 1 ≅ ∠ 7 and ∠ 4 ≅ ∠ 6 Proof Since k ∥ l , by the Corresponding Angles Postulate ,If two lines are intersected by a transversal, then alternate interior angles, alternate exterior angles, and corresponding angles are congruent The converse of the theorem is true as well If two corresponding angles are congruent, then the

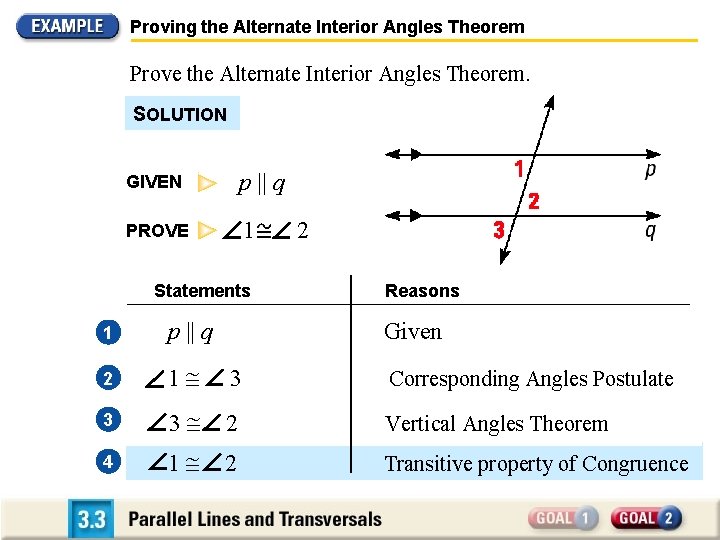
Example 3 Prove The Alternate Interior Angles Theorem Ppt Download

Postulates Theorems Ash1b Group

Alternate interior angles can be calculated by using properties of the parallel lines Example 1 Given two angles (4x – 19) 0 and (3x 16) 0 are congruent alternate interior angles Find the value of x and also determine the value of the other pair of alternate interior angles, Solution ⇒ 4x – 19 = 3x 16 ⇒ 4x – 3x = 1916= 4 x 35 – 19 = 121°Are consecutive interior angles so the sum is 180°

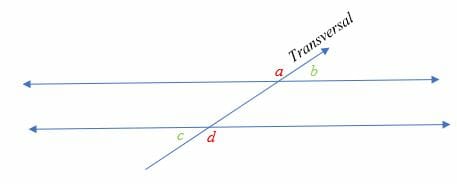
Alternate Exterior Angles Explanation Examples

Proof Of Alternate Interior Angles

Alternate Interior Angles Theorem Converse of the Alternate Interior Angles Theorem Converse of the SameSide Interior Angles Theorem SameSide Interior Angles Theorem 2 See answers Brainly User Brainly User Alternate Interior Angles Theorem Thank youu mason34 mason34Now, substituting the value of x in both the interior angles expression we get, (4x – 19)°Use the Corresponding Angles diagram to answer the question Diagram URL (remove spaces so that it can work) h t t p s / / p r n t s c/ g v v 9 k q 2 Which can be used to directly prove that ∠1 ≅ ∠8?

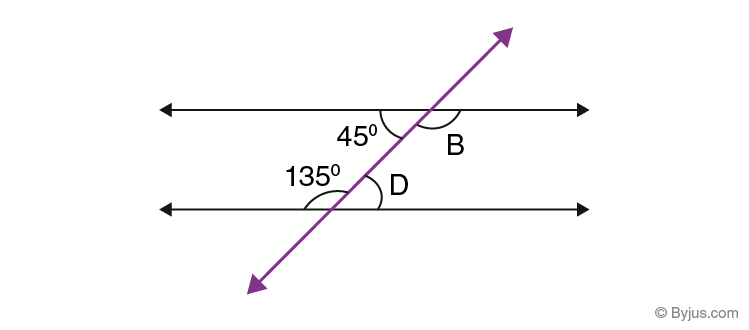
Alternate Interior Angles Definition Theorem Proofs And Examples

Proof Of Basic Theorem Of Corresponding Angles

Safety How works Test new features Press Copyright Contact us CreatorsThe Alternate Interior Angles Theorem states that, when two parallel lines are cut by a transversal , the resulting alternate interior angles are congruent So, in the figure below, if k ∥ l , then ∠ 2 ≅ ∠ 8 and ∠ 3 ≅ ∠ 5 Proof Since k ∥ l , by the Corresponding Angles Postulate ,4x – 3x = 16 19 x = 35°

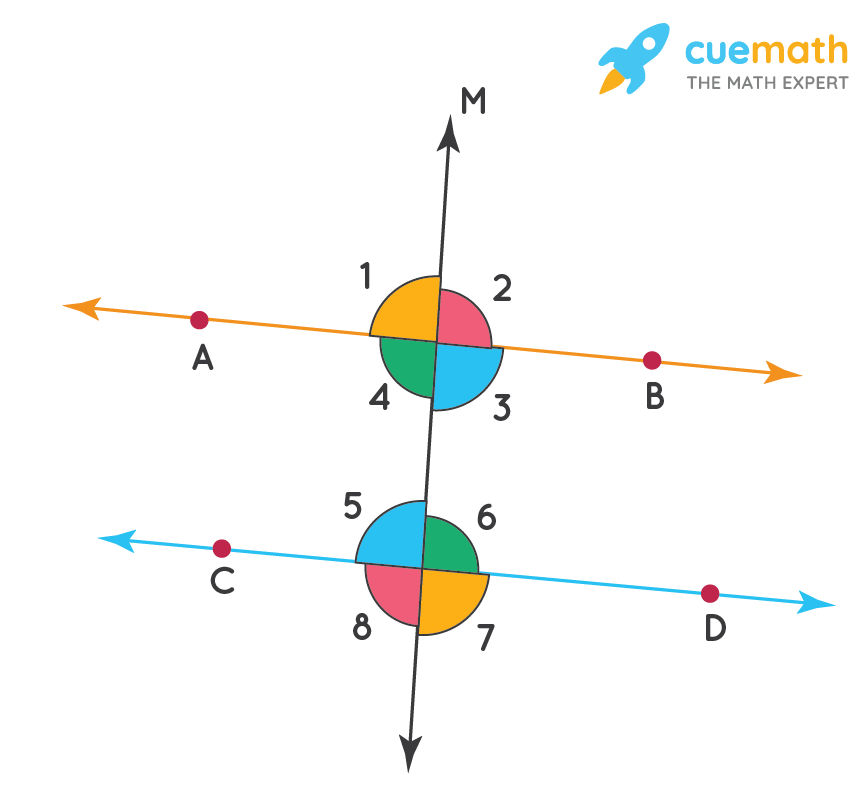
Alternate Exterior Angles Definition Theorem Proof Examples

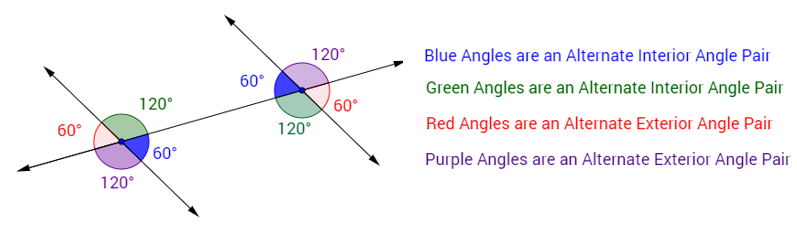
Alternate Interior Exterior Angles Video Lessons Examples Step By Step Solutions

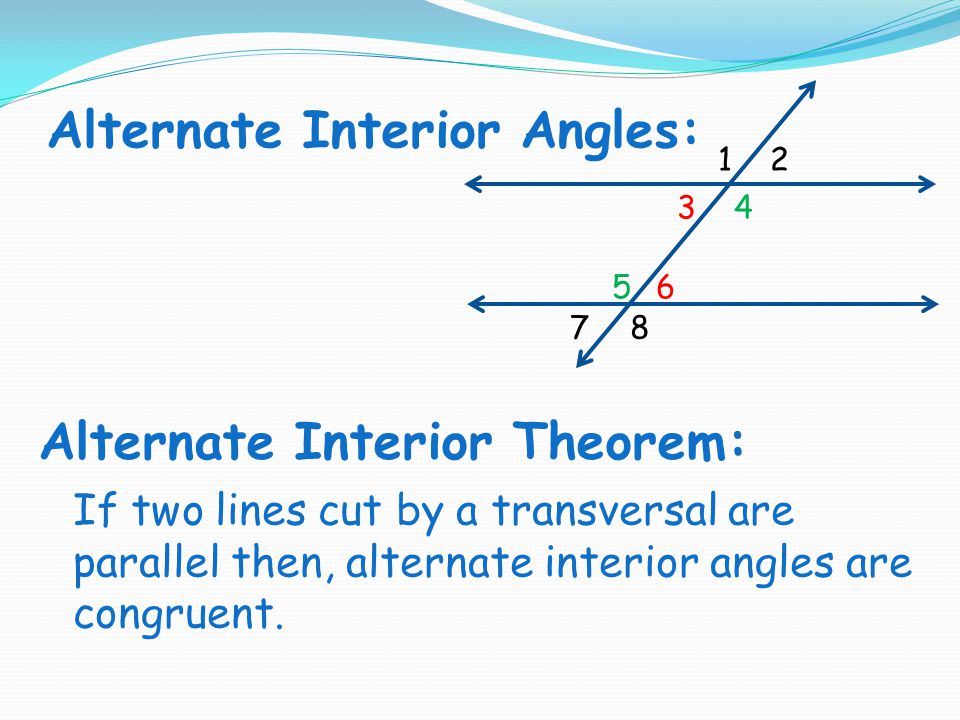
Objectives Define Transversal Alternate Interior Alternate Exterior Same Side Interior And Corresponding Angles Make Conjectures And Prove Theorems Ppt Download

Http Www Lyndhurstschools Net Userfiles 47 Classes 28 3 1 properties of parallel linespdf Pdf Id

West Side Geometry Exterior Angle Theorem

Alternate Exterior Angles Proof Youtube

Pin On Math

3

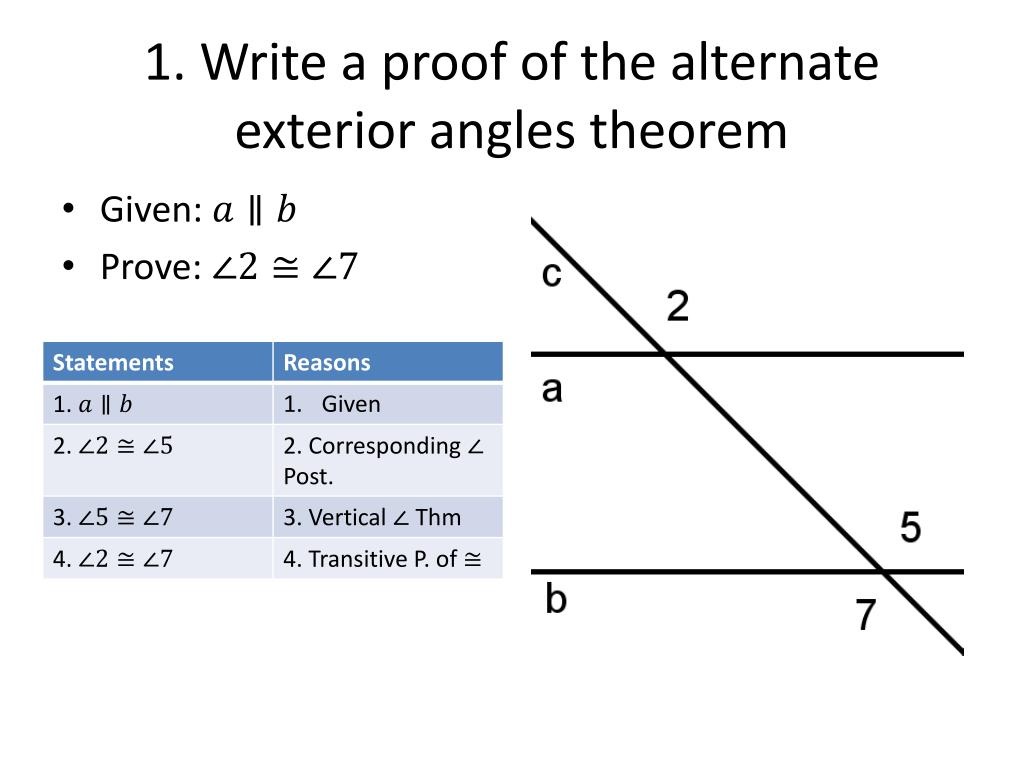
Ppt 1 Write A Proof Of The Alternate Exterior Angles Theorem Powerpoint Presentation Id 279

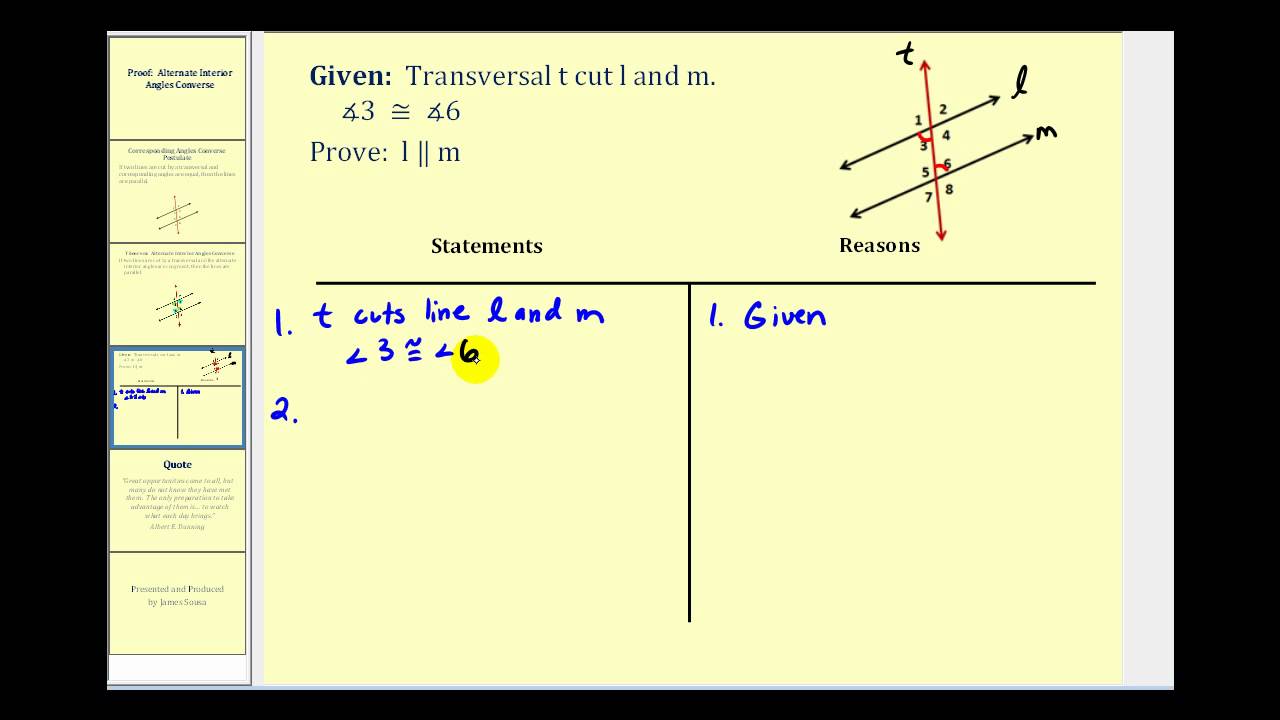
Proof Alternate Interior Angles Converse Youtube

Which Lines Are Parallel If M 3 M 6 Justify Your Answer A L M By The Converse Of The Alternate Interior Angles Theorem B R S By The Converse Of

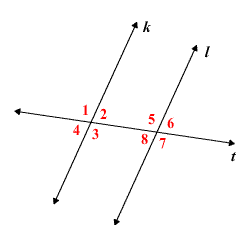
Alternate Interior Angles Theorem

Geo 3 4 Proving Lines Parallel

Alternate Exterior Angles Definition Theorem Video Lesson Transcript Study Com

Alternate Exterior Angles Read Geometry Ck 12 Foundation

Mrwadeturner Corresponding And Alternate Interior Angles

Write A Two Column Proof Of The Alternate Exterior Angles Theorem Given M N Prove 1 2 Homework Help And Answers Slader

Alternate Interior Angles Definition Theorem Examples Video

Same Side Interior Angles Proof Youtube

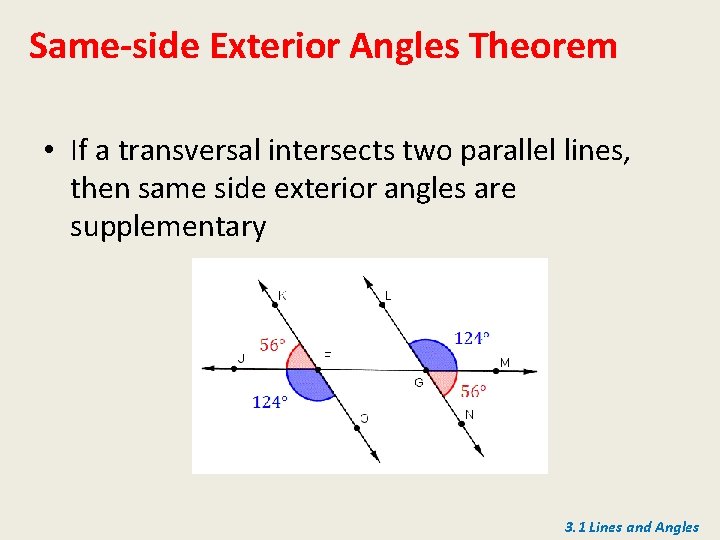
3 1 Lines And Angles Objective To Identify

Lines And M Are Intersected B See How To Solve It At Qanda

Given The Information In The Diagram Which Theorem Best Justifies Why Lines J And K Must Be Brainly Com

Theorem 6 2 Class 9 Alternate Interior Angles Are Equal

Alternate Exterior Angles Definition Theorem Video Lesson Transcript Study Com

Alternate Interior Angles Converse Theorem Wild Country Fine Arts

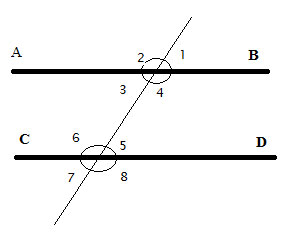
A Detailed Proof Of The Alternate Interior Angles Theorem Geometry Help

Given Xw Xy Xw Zy Prove Dwxz Dyzx A Alternate Interior Angle Theorem B Alternate Brainly Com

Http Www Pearlandisd Org Cms Lib Tx Centricity Domain 3000 4 3 proving lines are parallel Pdf

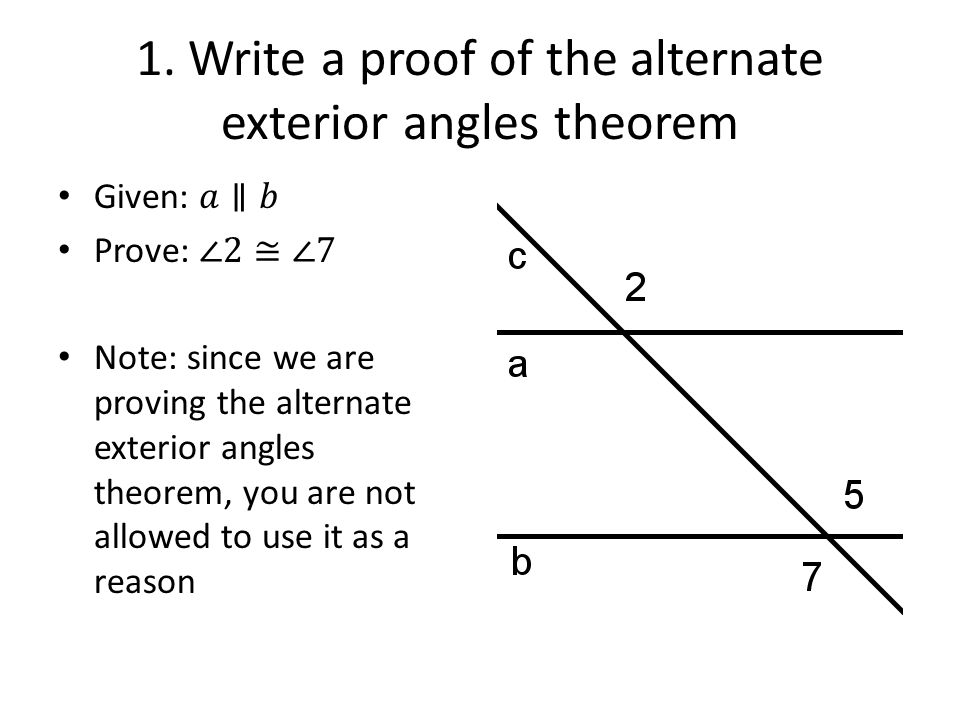
Alternate Interior Angles Theorem Wild Country Fine Arts

Example 3 Prove The Alternate Interior Angles Theorem Ppt Download

Corresponding Angles Postulate And Alternate Interior Angles Theorem Youtube

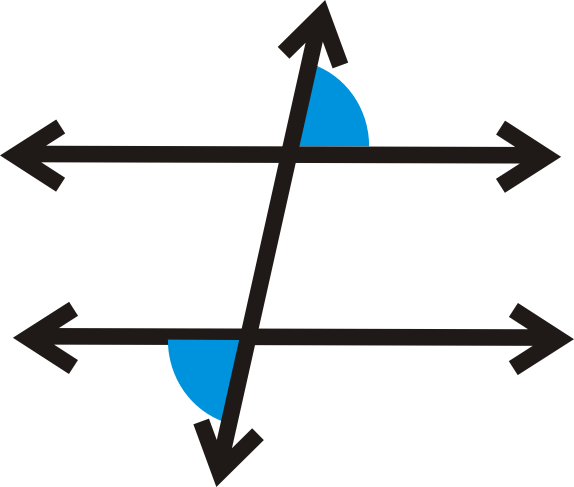
Alternate Exterior Angles Read Geometry Ck 12 Foundation

Alternate Interior Angles Definition Theorem Examples Video

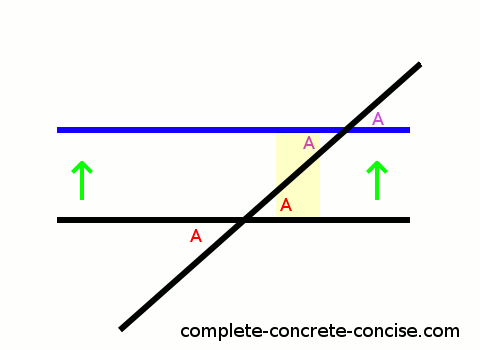
Proving Alternate Interior Angles Are Congruent The Same Complete Concrete Concise

Parallel Lines Cut By A Transversal Flip Book Notes Geometrycoach Com

Alternate Exterior Angles Definition Theorem Video Lesson Transcript Study Com

1

Theorem 6 3 If Alternate Angles Are Equal Then Lines Are Parallel

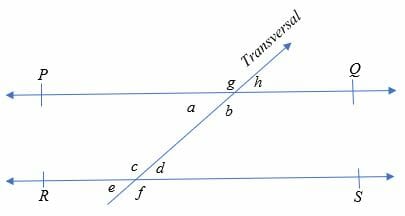
Alternate Interior Angles Explanation Examples

Prove The Alternate Interior Angles Theorem Fill Gauthmath

Same Side Exterior Angles Definition Theorem Video Lesson Transcript Study Com

Based On The Diagram Whi Descubre Como Resolverlo En Qanda

Activity 4 Complete The Proof Of The Alternate In Gauthmath

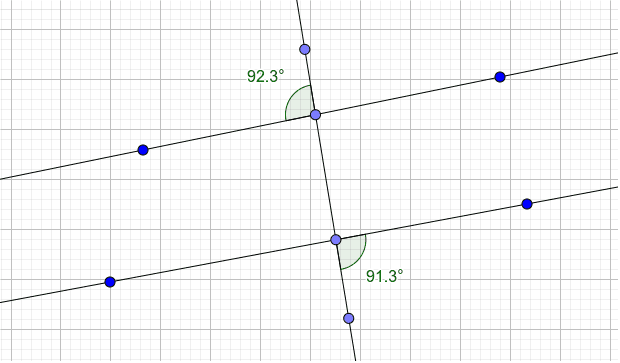
Alternate Exterior Angles Converse Theorem Geogebra

Converse Of Alternate Interior Angles Theorem Algebra And Geometry Help

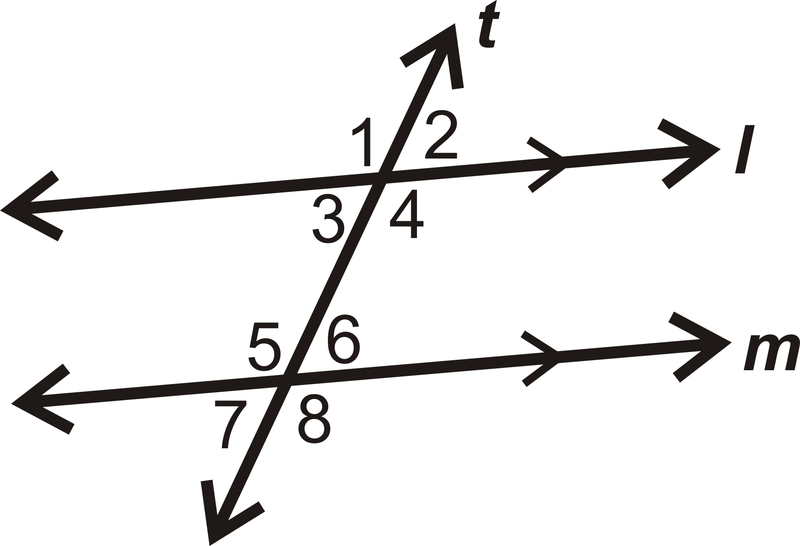
Alternate Interior Angles Read Geometry Ck 12 Foundation

Supply The Second Reason Complete The Following Proof Chegg Com

1 The Alternate Interior Angle Theorem States If Chegg Com

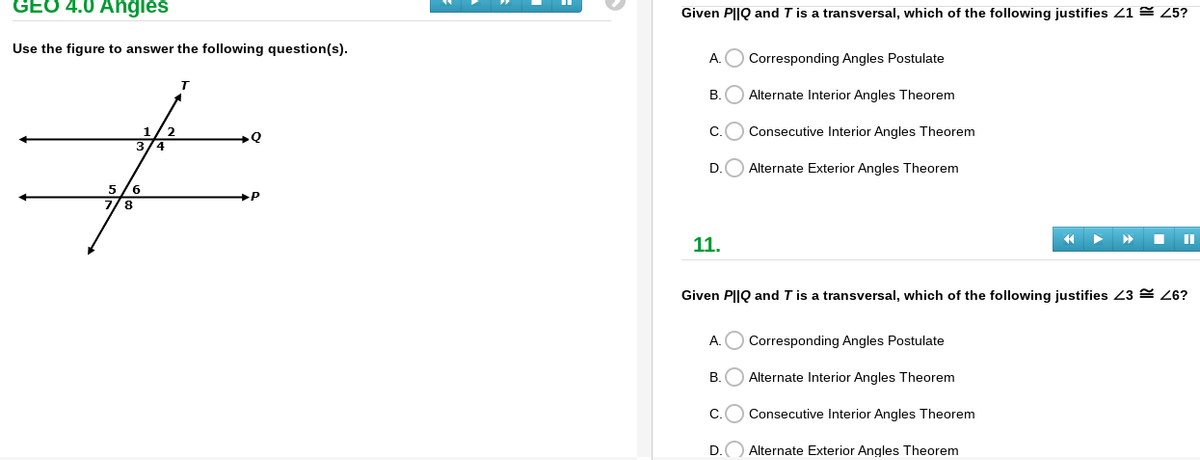
Answered Given P Iq And T Is A Transversal Bartleby

Swhsbarnhart Weebly Com Uploads 8 6 9 5 10 2 18 Geo 03 03 Notes Pdf

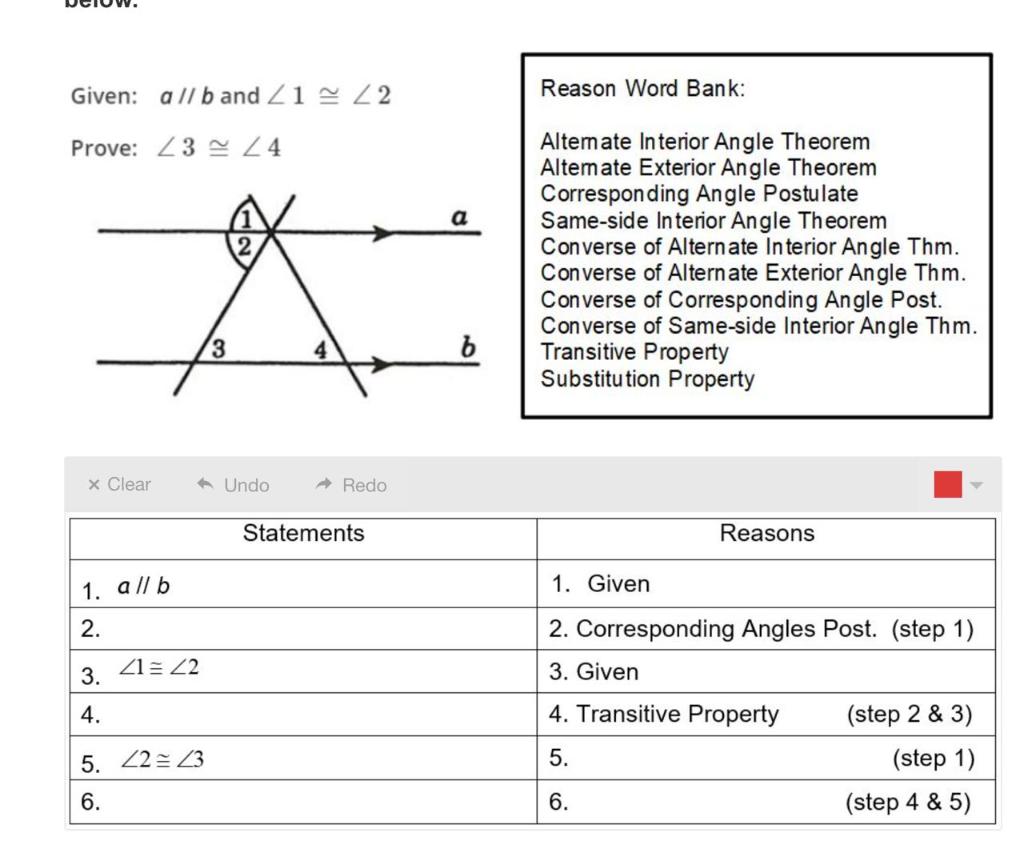
Given All Band 21 22 Reason Word Bank Prove Z3 Z4 Chegg Com

Example 3 Prove The Alternate Interior Angles Theorem

Q Tbn And9gcralrzrvpgfdofozovj117 G Rovfwmjlyfgbs2hz06lgofnu5z Usqp Cau

Consecutive Interior Angles Are Supplementary Wild Country Fine Arts

3 3 Proving Lines Parallel Objectives Students Will

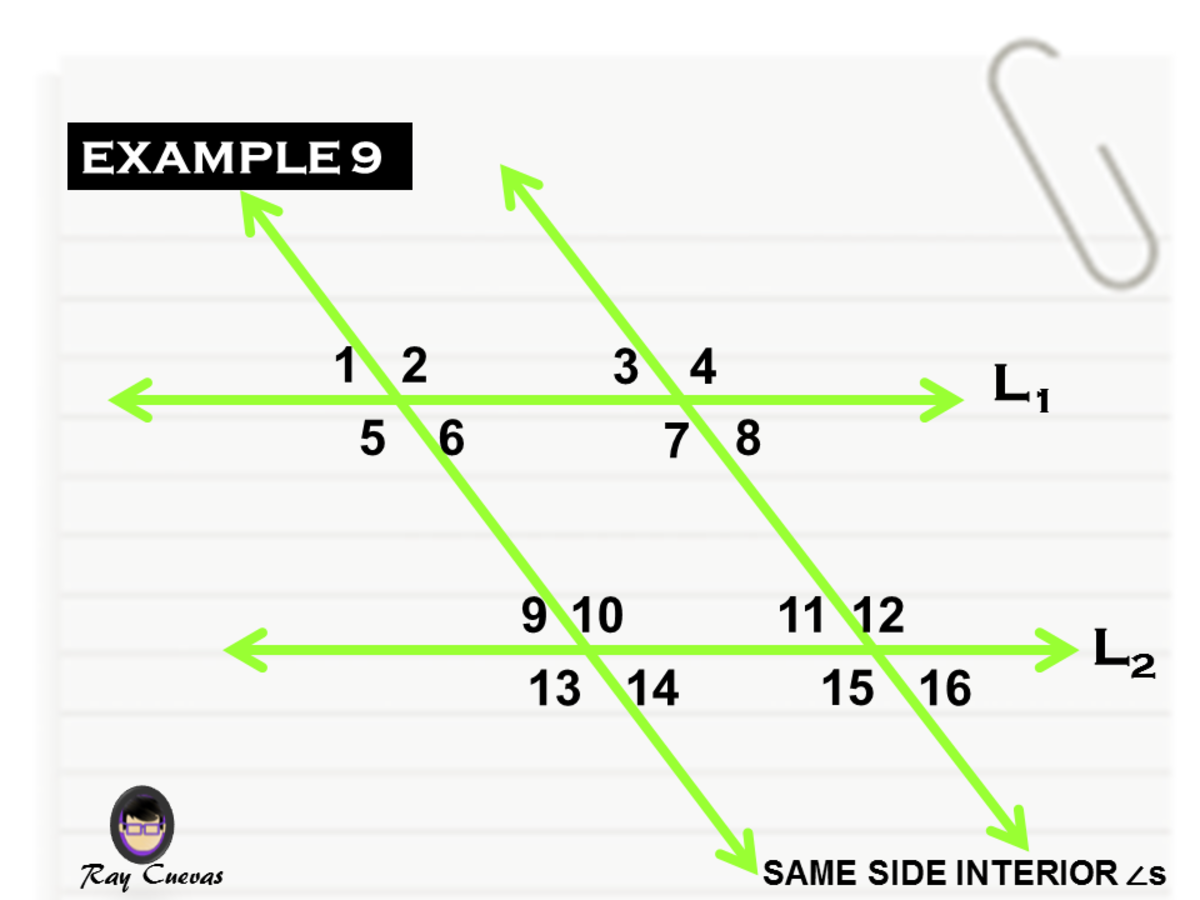
Same Side Interior Angles Theorem Proof And Examples Owlcation

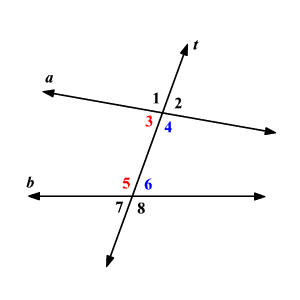
Consecutive Interior Angles Theorem

A Proof Of The Alternate Interior Angles Theorem Using Parallel Lines A And B With Transversal M Brainly Com

1 Name The Postulate Or Theor See How To Solve It At Qanda

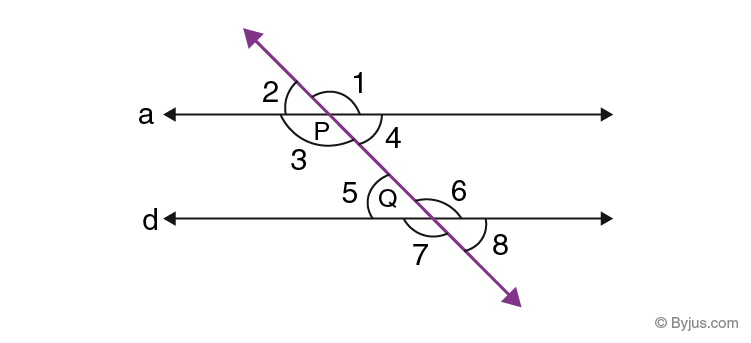
Alternate Interior Angles Definition Theorem Proofs And Examples

Unit 1 We Love Math

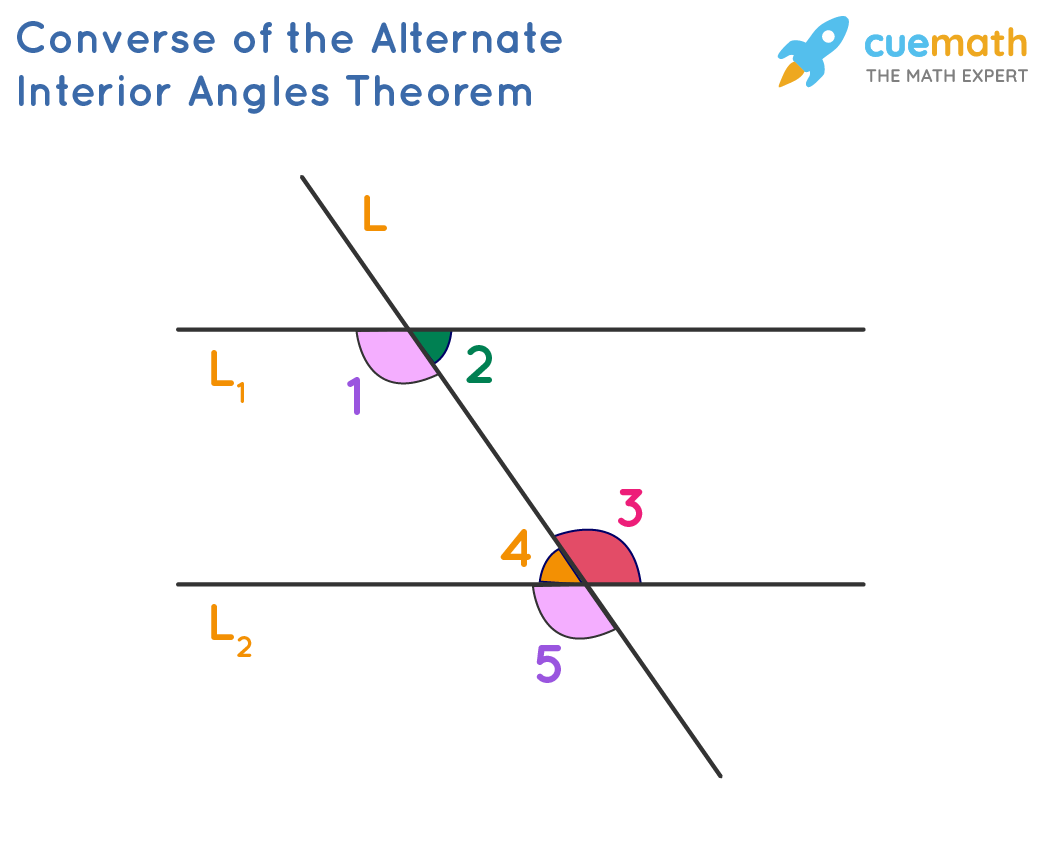
Alternate Interior Angles Definition Theorems Examples

Same Side Interior Angles Theorem Proof And Examples Owlcation

Alternate Interior Angles Definition Theorem More

Parallel Lines Transversal Theorems Flashcards Quizlet

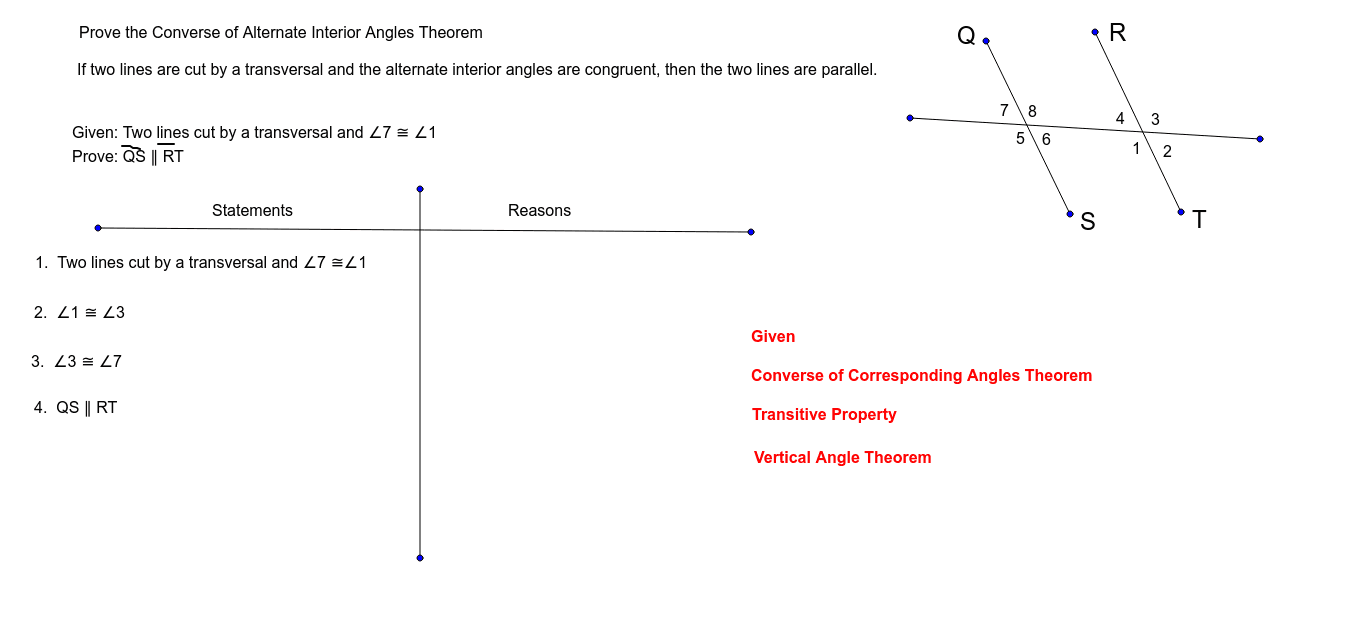
Prove Converse Of Alternate Interior Angles Theorem Geogebra

3 7 Same Side Interior Angles K12 Libretexts

Corresponding Angles Defintion Theorem Examples Video

Define Side Angles Same Interior

3 2 Proving The Converse Of The Alternate Interior Angles Theorem Algebra And Geometry Help

Alternate Interior Angles Proof Youtube

Mrwadeturner M1 Consecutive And Alternate Exterior Angles

Incoming Term: alternate interior corresponding angles theorem,